

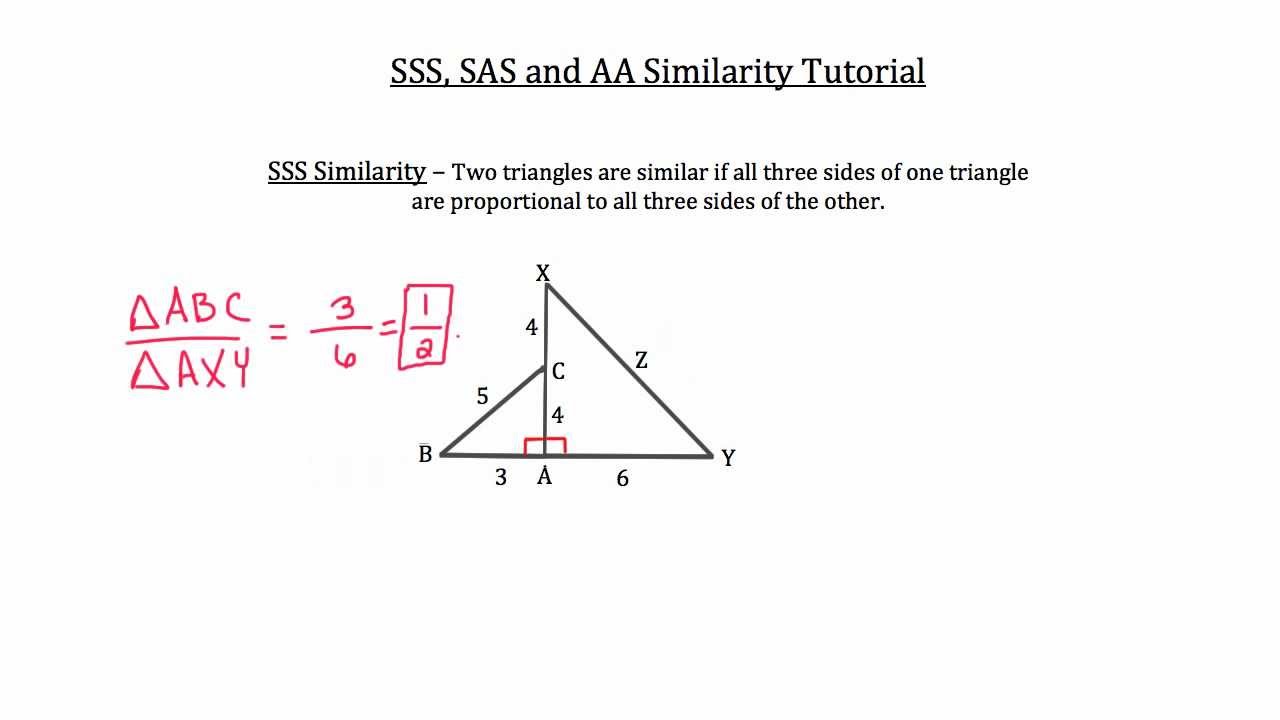
It is not necessary to check all angles and sides in order to tell if two triangles are similar. This is called the Side Angle Side Postulate or SAS. Side-Angle-Side If we can show that two sides and the included angle of one triangle are congruent to two sides and the included angle in a second triangle, then the two triangles are congruent. This is why there is no Side Side Angle (SSA) and there is no Angle Side Side (ASS) postulate. What about SSA (Side Side Angle) theorem? There is NO SUCH THING!!!! The ASS Postulate does not exist because an angle and two sides does not guarantee that two triangles are congruent. You might be interested: Question: What is cut out pressure? Why SSA is not a postulate? The Side Angle Side postulate (often abbreviated as SAS) states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent. The fundamental theorem of similarity states that a line segment splits two sides of a triangle into proportional segments if and only if the segment is parallel to the triangle’s third side.
(This is sometimes referred to as the AAA Postulate-which is true in all respects, but two angles are entirely sufficient.) The postulate can be better understood by working in reverse order. In Euclidean geometry, the AA postulate states that two triangles are similar if they have two corresponding angles congruent. How are the SAS ~ Theorem and the SAS Congruence Theorem alike? How are they different? Both use two pairs of corresponding sides and the included angles by those sides, but SAS ~ uses pairs of equal ratios, while SAS Congruence uses pairs of congruent sides. How are the SAS similarity theorem and the SAS congruence postulate alike? So, ∠X = ∠P, ∠Y = ∠Q, ∠Z = ∠R and XYPQ = YZQR = XZPR. Here, the two triangles XYZ and PQR are similar. If two triangles are similar then their corresponding angles are equal and corresponding sides are proportional. Side Angle Side Postulate The SAS Postulate tells us, If two sides and the included angle of a triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent. You might be interested: Often asked: How can I make my bathroom germ free? Is SAS a postulate?


 0 kommentar(er)
0 kommentar(er)
